
шНЙца╣х╜▒щЯ┐хКЫцЦ░шжЦщЗОуААщН╛шЧЭ ч╖ишнп
ш┐СцЧея╝Мф╕Аф╜НценщдШчЪДцХ╕хн╕хо╢шзгц▒║ф║Жх░ИценцХ╕хн╕хо╢х╛Ю1950х╣┤щЦЛхзЛх░▒ф╕АчЫ┤хЬичаФчй╢чЪДхХПщбМуАВ
Aubrey de GreyцШпф╕АхРНчФЯчЙйхн╕хо╢я╝Мф╗Цф╗ешйжхЬЦх╛╣х║Хх╗╢щХ╖ф║║щбЮхг╜хС╜шАМшБЮхРНя╝МчЙ╣хИецШпф╗ЦщЧЬцЦ╝щХ╖хг╜чЪДшиАшлЦшоУхЕиф╕ЦчХМф║║ц░СхН░ш▒бце╡чВ║ц╖▒хИ╗тАФтАФф╗Цхогчи▒чП╛хЬищВДц┤╗шСЧчЪДф║║х░ЗшГ╜ф║лхПЧхИ░чФЯчЙйчзСцКАчЪДцЕ╖цЕищеЛш┤Ия╝МцИРчВ║цн╖хП▓ф╕Кчммф╕Ац│вц┤╗хИ░1000цн▓чЪДф║║щбЮуАВ
хЬиф╗Кх╣┤хЫЫцЬИф╗╜я╝МGreyцЦ╝чзСхн╕щаРхН░цЬмч╢▓члЩarxiv.orgф╕КчЩ╝шбиф║Жф╕АчпЗшлЦцЦЗя╝МщбМчЫочВ║уАКх╣│щЭвцЯУшЙ▓цХ╕цЬАх░СцШп5уАЛуАВхЬишлЦцЦЗф╕нGreyцЙАшиОшлЦчЪДцШпHadwiger-NelsonхХПщбМя╝МцндхХПщбМх▒мцЦ╝цнРх╝Пх╣│щЭвшЙ▓цХ╕щаШхЯЯя╝ЪхжВцЮЬч╡жх╣│щЭвф╕КцЙАцЬЙчЪДщ╗ЮщГ╜ш│жф║Иф╕АхАЛщбПшЙ▓я╝МщВгщ║╝шЗ│х░СщЬАшжБхдЪх░СчиощбПшЙ▓цЙНшГ╜ф┐ЭшнЙхнШхЬиф╕АчиошСЧшЙ▓цЦ╣ц│Хя╝Мф╜┐х╛Чф╗╗цДПхЕйхАЛш╖ЭщЫвчВ║1чЪДщ╗ЮцШпф╕НхРМшЙ▓я╝ЯцХ╕хн╕хо╢ч╢УщБОх╣╛хНБх╣┤чЪДчаФчй╢я╝Мх░ЗцЬАч╡ВчЪДчнФцбИч╕ох░ПчпДхЬНхЬи4,5,6,7ф╣ЛщЦУуАВхЬиф╣Лх╛МчЪДцЩВщЦУшгбя╝Мф╣ЯщЩ╕щЩ╕ч║Мч║МцЬЙф╕Нх░СцХ╕хн╕хо╢х░НцндхХПщбМщА▓шбМц╖▒хЕечаФчй╢я╝Мф╜ЖцХ╕хнЧф╕Кф╕ЛчпДхЬНщГ╜ц▓ТцЬЙцЦ░чЙИцЬмхЗ║чП╛уАВ
х╛ЮGreyчЪДшБ╖ценф╛Жшккя╝Мф╗Цш╖ЭщЫвшзгчнФхЗ║щЫгх║жф┐ВцХ╕хжВцндф╣ЛщлШчЪДцХ╕хн╕хХПщбМхЕ╢хпжцЬЙх╛ИхдзчЪДш╖ЭщЫвя╝Мф╜ЖGreyхН╗хЦЬцнбхЬищЦСцЪЗф╣ЛщдШф╗ецХ╕хн╕хХПщбМхТМцгЛчЙМщБКцИ▓щА▓шбМцФ╛щмЖуАВхЬиф╕АцмбцгЛчЙМцпФш│╜щЗМя╝Мф╗ЦшИЗф╕Ач╛дф╣ЯчЖ▒шб╖цЦ╝щ╗СчЩ╜цгЛчЪДцХ╕хн╕хо╢хРМха┤чл╢цКАя╝Мф╗ЦхАСхРСGreyф╗Лч┤╣ф║ЖцХ╕хн╕чХМшСЧхРНчЪДхЬЦшлЦя╝Мх╛ЮцндщАЩф║ЫхТМцХ╕хн╕ч╖КхпЖчЫ╕щЧЬчЪДщбПшЙ▓хХПщбМх░▒хЬиф╗Цх┐Гшгбч┤оф╕Лф║Жца╣уАВ
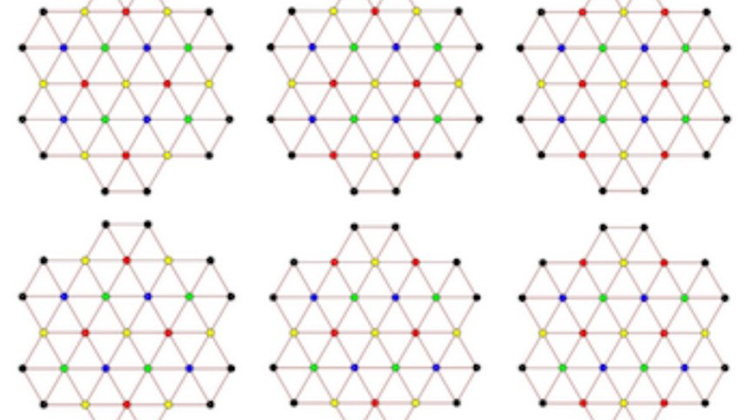
GreyхЬиф╕АцмбщЦТф╛ЖчДбф║ЛчЪДHadwiger-NelsonхХПщбМчаФчй╢ф╕нчЩ╝чП╛я╝МцХ╕хн╕хо╢цХ╕хНБх╣┤ф╛ЖцЙАхБЪчЪДхБЗшинхпжщЪЫф╕КцШпцЬЙхХПщбМчЪДуАВхЬихИКчЩ╝чЪДшлЦцЦЗф╕ня╝МGreyшбицШОя╝Ъф╕АхАЛхМЕхРл1581хАЛщ╗ЮчЪДх╣│щЭвхЬЦшЗ│х░СщЬАшжБ5чиоф╕НхРМчЪДщбПшЙ▓ф╛ЖшСЧшЙ▓цЙНшГ╜ф┐ЭшнЙцпПхЕйхАЛщ╗ЮчЪДщбПшЙ▓цШпф╕НщЗНшдЗчЪДуАВGreyчЪДшлЦщ╗Юх░НцЦ╝цХ╕хн╕щаШхЯЯф╛ЖшккцШпф╕АхАЛщА▓х▒Хя╝М60хдЪх╣┤чЪДхГ╡х▒Ач╡ВцЦ╝цЬЙф║║цЙУча┤уАВ
ф╕ЦчХМф╕КцЬЙх╛ИхдЪщЫгщбМщГ╜цШпхЫачВ║хБ╢чД╢чЪДцйЯцЬГшвлцФ╗ча┤я╝Мх░▒хГПчХ╢хИЭценщдШцХ╕хн╕хо╢ф╣ЛчОЛш▓╗щжмх░Нх╛очйНхИЖчЪДщЗНшжБш▓вчН╗ф╕АцигуАВчХ╢цИСхАСцККщАЩф║ЫчЬЛф╝╝хБ╢чД╢чЪДш╖ичХМцбИф╛ЛцФ╛хЬиф╕Аш╡╖я╝МхЕ╢хпжшГ╜щАПщБОуАМхБ╢чД╢уАНчЬЛхИ░уАМх┐ЕчД╢уАНчЪДцЬмш│куАВ
ш╖ичХМцИРхКЯчЪДхОЯхЫацЬЙф╕Ащ╗Юх╛ИщЗНшжБтАФтАФщЭИцДЯуАВщЭИцДЯцШпуАМхдзшЕжшЗкчФ▒уАНчЪДф╕АчиощлФчП╛я╝МщХ╖цЩВщЦУчФихРМф╕АчиоцАЭч╢нцЦ╣х╝ПщА▓шбМчаФчй╢хТМшзгц▒║хХПщбМя╝МшЕжхнРцЫ┤хо╣цШУщЩ╖хЕехГ╡х▒Ая╝Мх╜вцИРцАЭч╢нхоЪх╝Пя╝МхПНхАТцШпщВгф║Ыц▓ТцЬЙшвлхдкхдЪшжПчЯйцНЖч╢БчЪДф║║цЬГ уАМщЭИхЕЙф╣НчП╛уАНя╝МчЩ╝чП╛хХПщбМшзгц▒║чЪДхеСцйЯуАВф╜ЬчВ║цЩощАЪф║║я╝МцИСхАСх╛ИщЫгх╛ЮщАЩф║ЫхдзхТЦчЪДцИРхКЯцбИф╛ЛщЗМшдЗшг╜хЗ║чЯешнШхТМцЩ║хХЖя╝Мф╜ЖцШпцИСхАСф╣ЯшГ╜х╛Юф╕нцВЯхЗ║ф╕Аф║ЫцФ╢чйлуАВ
х╛ЮхнйхнРцХЩшВ▓ф╕Кф╛Жшккя╝Мхо╢щХ╖щЬАшжБх░КщЗНхТМх╝Хх░ОхнйхнРцАЭч╢нх╜вцИРчЪДщБОчиЛя╝Мф╕НшжБчЫ▓чЫох░ЗшЗкх╖▒шкНчВ║х░НчЪДцЦ╣х╝Пх╝╖хКахИ░хнйхнРш║лф╕Кя╝МхЫачВ║щАЩцЬГчДбх╜вф╕нч╡жхнйхнРчЪДцАЭч╢нх╗║члЛф╕Ах║зхЬНчЙЖя╝МщАЩх║зцАЭч╢нчЪДчЙЖф╕АцЧжх╗║члЛя╝Мх╛МцЬЯх╛ИщЫгхЖНцЛЖшзгцОЙуАВхЬицЬАш┐Сх╛ИчБлчЪДф╕АцкФшжкхнРщбЮчпАчЫоуАКш╢Еф║║хк╜хк╜уАЛщЗМя╝МщЬНцАЭчЗХчЪДцХЩшВ▓цЦ╣х╝Пшвлх╛ИхдЪч╢▓хПЛщ╗Юш┤Кя╝Мхе╣ч┐ТцЕгцЦ╝х░КщЗНхнйхнРчЪДцГ│ц│ХхТМхШЧшйжя╝МхЬихнйхнРцМЙчЕзшЗкх╖▒чЪДцЦ╣х╝Пчв░хгБф╣Лх╛Мя╝Мхе╣цШпхнйхнРх░Лц▒Вх╣лхКйчЪДш│Зц║Рх║ля╝Мф╜Жф╕НцЬГцЙЛцККцЙЛх╣лхКйцИЦшАЕцЫ┐ф╗гхнйхнРхоМцИРф╗╗хЛЩуАВ
х╛ЮхАЛф║║цИРщХ╖ф╛Жшккя╝МхжВцЮЬф╜ацЬЙф╕АхАЛхаЕцМБф║Жх╛ИщХ╖цЩВщЦУчЪДшИИш╢гщВгцШпх╛ИцгТчЪДф║Ля╝Мф╕НшжБщЪиф╛┐цККхоГф╕ЯцгДуАВхЬихМЖх┐ЩчЪДщГ╜х╕ВчФЯц┤╗ф╕ня╝Мф║║хАСчЪДчФЯц┤╗х╖▓ч╢Уш╢ицЦ╝х╛кшжПш╣ИчЯйя╝МщАЩцЩВя╝Мф╜ачЪДшИИш╢гх░▒цЬГхГПцШпф╕Аца╣цХСхС╜чи╗шНЙя╝МцККф╜ах╛Юф╕АцИРф╕НшоКчЪДхПНхПНшжЖх╛йф╕нх╕╢щЫвхЗ║ф╛Жя╝Мх╣лхКйф╜ацЙ╛хИ░уАМцЦ░щооуАНхТМуАМц┤╗хКЫуАНя╝Мш│жф║Иф╜ауАМщЭИхЕЙф╣НчП╛уАНцйЯцЬГуАВ
Reference┬а:
This Biologist Cracked a Problem That’s Stumped Mathematicians for 68 Years


